最近在对别人的程序做可视化封装,稍微涉及到了一点正则表达式,有感而发,写下这篇。
举个例子 匹配端口号,众所周知 端口号的范围是0-65535。但是端口0不常用,所以一般性认为端口号是从1-65535.
那我们应该如何用正则表达式匹配端口号呢?(省流:\b(6553[0-5]|655[0-2]\d|65[0-4]\d{2}|6[0-4]\d{3}|[1-5]\d{4}|[1-9]\d{0,3})\b)
写正则表达式的第一步是分层,准确点来说是分类,这样会给你的书写带来极大地帮助,不然就是一团浆糊
那么端口号可以简单分为以下几层
| 第一层 | 65530-65535 |
| 第二层 | 65500-65529 |
| 第三层 | 65000-65499 |
| 第四层 | 60000-64999 |
| 第五层 | 10000-59999 |
| 第六层 | 1000-9999 |
| 第七层 | 100-999 |
| 第八层 | 10-99 |
| 第九层 | 1-9 |
是不是看着有点吓人?
别慌,我们来简化一下,可以发现第六七八九层格式一样,所以我们可以化简一下,第六七八九合为一层,也就是1-9999
于是我们最终得到了这张分层表
| 第一层 | 65530-65535 |
| 第二层 | 65500-65529 |
| 第三层 | 65000-65499 |
| 第四层 | 60000-64999 |
| 第五层 | 10000-59999 |
| 第六层 | 1-9999 |
下面是分层依据,可能有点难以理解,如果真无法理解,那就跳到构造表达式去。不过如果思路都搞不懂的话,都是没有用的
下面说说分层思路,有一个规则是不变的,就是从复杂到简单
首先观察下范围:1-65535
最特殊的是什么?
当然是65535这个数字
那我们推广一下。
如果有一个数字,它的格式为6553x,那是不是最后那个x只能是0-5?
好,第一层分完了,是不是很简单?
接下来继续向下分,应为6553x已经分了出去,剩下1-65529
同第一层一样,如果有一个数字,它的格式是655xy
那么这个x只能0,1,2,而y可以是0-9中的任何一个数字。
这里跳跃有点大,可以仔细想想
到此第二层也分完了。
现在范围变成了 1-65499
还是同理,就是照着这个逻辑分下去,我就不再赘述了,免得有人说水。
这个地方很重要,需要好好揣摩。学习正则表达式的核心之一,就是要学会拆分对象。
那么接下来开始正式写正则表达式
之前,推荐一个网站https://regex101.com/,可以测试正则表达式,挺好用的
那么下面正式开始
第一步拿出我们的分层表,嗯,第一层是 65530-65535
那么也就是前面四个数是6553固定,最后一个取0-5,翻译过来就是:6553[0-5]题外话:正则的语法我不再赘述,自己搜索去
第一层结束后看第二层 从65500 - 65529
还是分析,前三个数是655不动,第四个取0-2,最后一个数任意,翻译过来就是:655[0-2]\d
第三层是65000-65499
还是老方法,但又有点不同,最后两位都可以随便取,所以匹配两次,也就是:65[0-4]\d{2}
第四层是60000-64999
这就更简单了,一通操作得:6[0-4]\d{3}
第五层则是10000-59999
这个跳的有点大,表面上好像看不出什么,但是仔细看会发现,第一位是1-5,后面不管了
翻译过来就成了:[1-5]\d{4}
最后一层,1-9999
“啊,这不有手就行?\d{1,4}”
错,端口号开头不能是0,所以应该是[1-9]\d{0,3}
好完事具备,我们把这些全部用 “|” 连在一起,然后试试看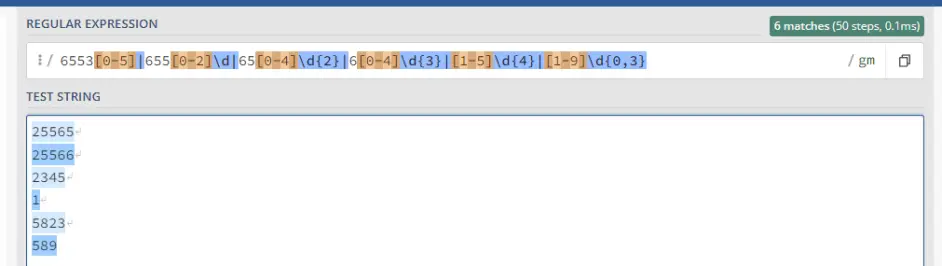
看上去运行的不错,但是.... 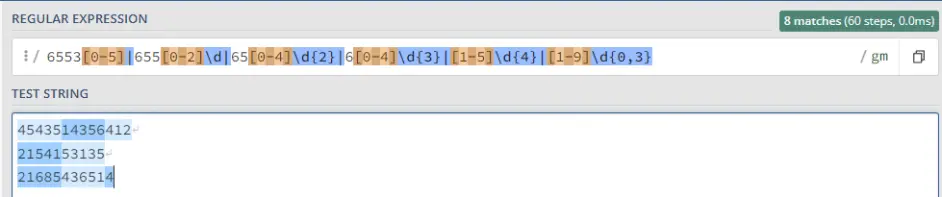
What?这什么情况?
莫慌,我们看一下右边的分步 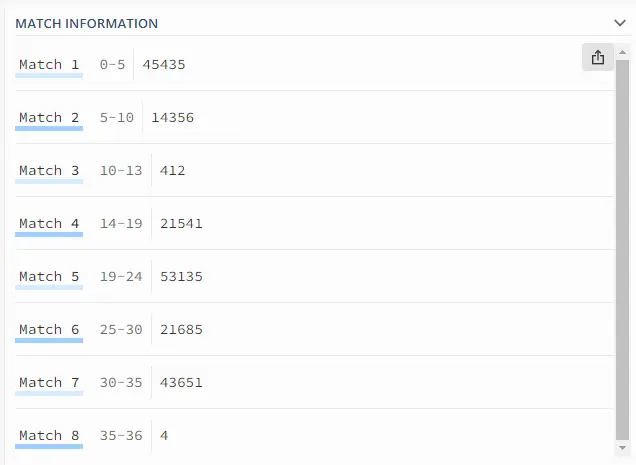
原来是多次匹配了,如何解决这个问题呢?
很简单,只要加个()表示这一长串表达式是一个集合,然后用^或者$表示从头或者从尾匹配一次就行了
当然你也可以^ 和$ 一起用表示整行匹配
^或者$ 可以替换为\b,在这个表达式上效果是一样的,但不能一概而论。
如果只在头加,或者只在尾加,表示的是匹配一个匹配的结果
但是我要的是判断是否合规,不是匹配合格的结果,所以我在头尾加上\b
表达式就变成了
\b(6553[0-5]|655[0-2]\d|65[0-4]\d{2}|6[0-4]\d{3}|[1-5]\d{4}|[1-9]\d{0,3})\b
当然
^(6553[0-5]|655[0-2]\d|65[0-4]\d{2}|6[0-4]\d{3}|[1-5]\d{4}|[1-9]\d{0,3})$
这样也是可以的,在这个正则表达式里效果是一样的,不过一般^ 和$不是用来干这事的就是了。
现在写完正则表达式,再看一开始的分组,可以想象一下如果没有分组,该如何写这个正则表达式。那真的是一筹莫展,无处下手。分组分类思想在正则表达式中的重要性可见一斑